مثلاً شکل یک مربع با یک قطر را مجسم کنید؛ به راحتی میتوان آنرا بدون برداشتن قلم از روی کاغذ کشید. اما اگر بخواهیم مربع با دو قطرش را به گونهای بکشیم که از ضلعها یا قطرهایی که رسم شده دوبار عبور نکنیم کار مشکل میشود، نه؟
سالها پیش شخصی به نام «اویلر» برای اولین بار مسئله ای به عنوان «پل کوینزبرگ» را مطرح کرد که زمینه شاخه مهمی از ریاضیات به نام «نظریه گرافها» شد. او میخواست از تمام پلهای شهرش بگذرد، طوری که فقط یک بار از هرکدام آنها عبور کند!
شما هم برای اینکه با این مبحث جالب بیشتر آشنا شوید ،کاغذ و قلم را بردارید و تلاش کنید شکلهای آخر مطلب را به همین روش بکشید.
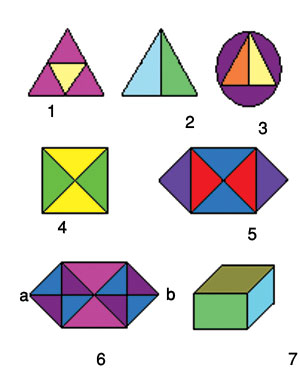
اگر محل تلاقی چند خط را یک نقطه بنامیم، نقطه فرد به نقطه ای گفته میشود که تعداد خطهایی که به آن وصل است فرد باشد و نقطه زوج هم به نقطه ای گفته می شود که تعداد خطهایی که به آن وصل شده است زوج باشد. مثلاً در شکل شماره یک، 6 نقطه داریم که همه آنها زوج هستند.
با دلیل ریاضی میتوان نشان داد که اگر شکل، دارای هیچ نقطه فردی نباشد و یا تعداد نقطههای فرد آن 6،4،2....(عددی زوج) باشد، آن شکل قابل ترسیم است. مثلاً شکلهای 1 و 5 را از هر راسی که شروع کنید به راحتی میتوانید بکشید.
اگر شکل، دو نقطه فرد داشته باشد (شکلهای 2و 3و 6) باز هم قابل کشیدن است، اما به شرط این که از نقطه فرد شروع به کشیدن کنید. مثلاً در شکل 6، اگر از نقطه ای به جز نقطههای a و b شروع کنید نمیتوانید شکل را بهطور کامل رسم کنید. و اگر شکل بیشتر از دو نقطه فرد داشته باشد (شکل 4و7) ، هرگز نمیتوانید آن را رسم کنید و تلاش شما بینتیجه خواهد بود.